ExploreLearning Gizmos: Math & Science Virtual Labs and Simulations
Gizmo of The Week
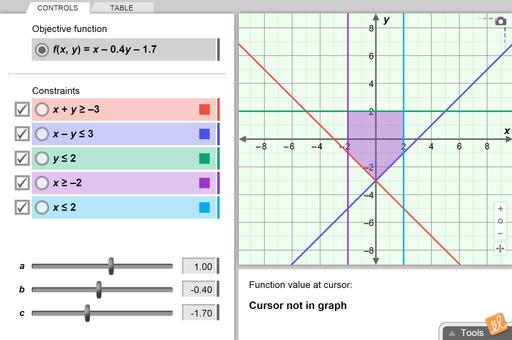
Linear Programming
Linear programming is a method used to determine the best outcome (such as maximizing profit or minimizing cost) given certain requirements. It was developed independently by Soviet and American mathematicians during World War II and was used to optimize resource allocation and transportation. The method was kept secret until it was published by George Dantzig in 1947. Once the method was made public, many industries began using it to manage time and resources. Today, it is widely used in business, economics, and engineering.
Linear programming simplifies complex problems by breaking them down into smaller, more manageable pieces. In a linear programming problem, the outcome is described by the objective function and the constraints (requirements) are represented by a system of linear inequalities.
In the Linear Programming Gizmo, students use the graph of a feasible region with up to five constraints to find the maximum or minimum of an objective function. The feasible region is the graph of the system of constraints, and it contains all (x, y) points that meet the requirements. The maximum or minimum value of the objective function will always occur at a vertex of the feasible region.
Linear programming is a method used to determine the best outcome (such as maximizing profit or minimizing cost) given certain requirements. It was developed independently by Soviet and American mathematicians during World War II and was used to optimize resource allocation and transportation. The method was kept secret until it was published by George Dantzig in 1947. Once the method was made public, many industries began using it to manage time and resources. Today, it is widely used in business, economics, and engineering.Linear programming simplifies complex problems by breaking them down into smaller, more manageable pieces. In a linear programming problem, the outcome is described by the objective function and the constraints (requirements) are represented by a system of linear inequalities.In the Linear Programming Gizmo, students use the graph of a feasible region with up to five constraints to find the maximum or minimum of an objective function. The feasible region is the graph of the system of constraints, and it contains all (x, y) points that meet the requirements. The maximum or minimum value of the objective function will always occur at a vertex of the feasible region.
